01 | Deterministische endliche Automaten (DEA)

1. 👤 Öffne FLACI und lege dir einen eigenen Account an, damit deine Ergebnisse dort gespeichert werden. (Das ist einfacher, als die JSON-Dateien für die Automaten jeweils herunterzuladen.)

   ⏬Automat 1: Was bestimme ich?

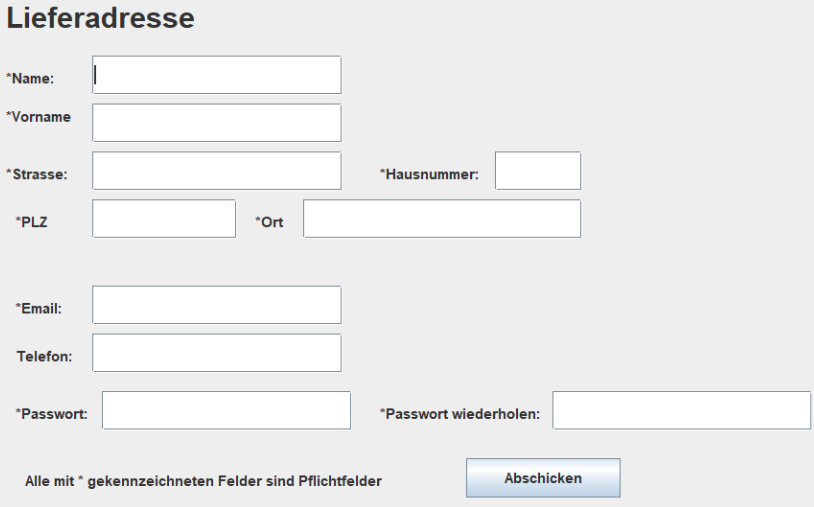
2. 👤 Öffne den Automaten 1 in Flaci. Über die Schaltfälche „Simulation“ kannst du verschiedene Eingaben ausprobieren. Ermittele durch Eingabe verschiedener Wörter, bei welchen Eingaben die Simulation grün leuchtet und bei welchen rot. Welches Eingabefeld des Web-Formulars wird mit dem Automaten überprüft?

3. 👤 Notiere stichwortartig, welche Elemente bei der Verarbeitung eines Wortes beteiligt sind. Beschreibe auch den Unterschied zwischen einfach und doppelt umkreisten „Kreisen“ (so genannte „Zustände“).

   ⏬Automat 2: Was bestimme ich?

4. 👤 Öffne den Automaten 2 und vergleiche das Verhalten des zweiten Automaten mit dem des ersten. Überlege dir einen Grund dafür, einen Automaten wie den zweiten einzusetzen.

5. 👤 Verändere den zweiten Automaten so, dass nur solche fünfstellige Ziffernfolgen als Eingabeworte akzeptiert werden, die

   • mit einer beliebigen un­geraden Ziffer starten oder
   • die auf eine durch drei teilbare Ziffer enden.

   🏃‍♀️‍➡️ Extras: Setze beide Anforderungen um!

Ein DEA wird formal durch ein 5-Tupel definiert:

🤔 Ist ein DEA ein Transduktor oder ein Akzeptor?

🖼️ Beispielbild

1. 👤 Erstelle einen Automaten, der ein weiteres Eingabefeld über­prüft. Du kannst dir eines der folgen­den Fel­der aussuchen (angeordnet von etwas leichter nach etwas schwieriger):

   • Variante 1: Korrekte Vornamen
   • Variante 2: Korrekte Hausnummern
   • Variante 3: Korrekte E-Mail-Adresse

   Beachte, dass sich die Zeichenmenge (das so genannte Alphabet) jetzt ändert: Es gibt nicht mehr nur Ziffern, sondern auch Buchstaben. Das Alpha­bet kannst du auf FLACI selbst umstellen. Zur Hilfe gibt es unten Vorlagen, die du benutzen kannst. (Die Vorlagen sind leider nicht ideal: Bei der Vorlage zu den Vorname gibt es z. B. nur die Buchstaben a–z und A–Z; verschiedene Vornamen sind damit nicht darstellbar, z. B. Bülent, Çağla, Tomáš uvm.)

   💁 Hilfen | Vorlagen für Automaten ⏬Vorlage für Variante 1 ⏬Vorlage für Variante 2

   💁 Hilfen

   • Damit es nicht zu unübersichtlich wird, kannst du so tun, als wenn es z. B. nur vier Klein- und Großbuchstaben gäbe, al­so a, b, c, d, A, B, C, D.
   • Tipp: Den Zustand, den du beim einem zu akzeptierenden Wort am Ende erreichen willst, musst du per Rechtsklick als Endzustand bezeichnen. (Es kann auch mehrere Endzustände geben.)
   • Tipp: Es kann nützlich sein, einen so genannten Fehlerzustand (oder Trap-Zustand) zu benutzen. Das ist ein Zustand, aus dem die Zustandsabfolge nicht mehr „herauskommt“; dann wird das Wort auf jeden Fall verworfen.

2. 👥👥 Schaut euch im Klassenraum nach einer anderen Gruppe um, die bereits fertig ist, und wechselt die Plätze. Testet dann den Automaten der anderen Gruppe mit verschiedenen Eingaben. Stimmt alles?

3. 👥 Bereitet euch darauf vor, euren Automaten zu präsentieren.

1. Jede Person bekommt die Darstellung eines DEA und hält sie sich – ohne darauf zu schauen! – an die Stirn.

   👥 Stellt euch mit Hilfe der Fachbegriffe vorne an der Tafel gegenseitig Fragen zu euren Automaten und er­mittelt auf diese Weise, wie genau euer DEA beschaffen ist. Wer zuerst seinen DEA korrekt notiert hat, hat gewonnen. Anders als bei dem echten Spiel „Wer bin ich?“ dürft ihr auch Fra­gen stellen, die andere Antworten als Ja und Nein haben.

   💁 Hilfen

   • Eine Frage könnte etwa sein: „Wie viele Zustände habe ich?“ oder „Ist der Zustand q1 ein akzeptierender Zustand?“

2. 👥 Zeigt, dass der DEA von Person 1 das Wort $abbba$ akzeptiert, indem ihr die Zustandsabfolge in der folgenden Form darstellt: $Z_1 \xrightarrow{a} Z_2 ...$

3. 👥 Begründet, dass der zweite DEA jedes Wort, in dem 2025 Nullen enthalten sind, nicht akzeptiert.

   💁 Hilfen

   • Wenn man auf Anhieb keine Idee hat, kann es hilfreich sein, die Aufgabe für einfachere Fälle zu bearbeiten: Wie sieht es aus, wenn eine Null im Wort enthalten ist, zwei Nullen, drei Nullen usw.? Wenn man so vorgeht, erkannt man oft ei­ne Regel und kann die ursprüngliche Aufgabe lösen.

4. 👥 Analysiert die beiden Automaten und bestimmt, welche Wörter jeweils von ihnen akzeptiert werden. Beschreibt eure Ergebnisse so präzise wie möglich!

5. Die Übergangsfunktion eines Automaten kann man mit Hilfe eines Übergangsgraphen darstel­len; das ist die Darstellung, die wir bisher verwendet haben. Man kann die Übergangsfunktion aber auch als Überga­ngstabelle angeben. Hier seht ihr die Übergangstabelle für den ersten DEA:

   $d$	$a$	$b$
   $Z_1$	$Z_2$	TRAP
   $Z_2$	$Z_3$	$Z_2$
   $Z_3$	TRAP	TRAP
   TRAP	TRAP	TRAP

   • 👤 Erstelle eine entsprechende Übergangstabelle für den zweiten DEA.
   • 👥 Wägt Vor- und Nachteile der beiden Darstellungen gegen­einander ab.

🏃‍♀️‍➡️ Extras: Erstelle einen DEA über dem Eingabealphabet $A = \{0, 1\}$, der genau solche Zahlen in Binärzahldarstel­lung akzep­tiert, die durch Vier teilbar sind.

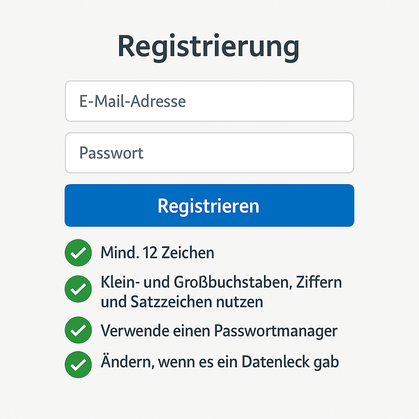
Gegeben ist das Eingabealphabet: $A = \{ a, b, c, 0, 1, 2, \#, *, ! \}$. Ein Eingabewort (Passwort) soll genau dann akzeptiert werden, wenn es mindestens einen Buchstaben, mindestens eine Ziffer und mindestens ein Sonderzeichen enthält.

1. 👤 Erweitere den vorgegebenen Automaten geeignet!

   🤯 einfacher🥵 schwieriger

   Hier müssen die Übergänge beschriftet werden.

   ⏬Passwortautomat - Vorlage 1

   Hier müssen Zustände und Übergänge ergänzt werden.

   ⏬Passwortautomat - Vorlage 2

2. 👤 Verändere den Automaten so, dass er über dem Eingabealphabet $A = \{b, z, s\}$ arbeitet. Dabei steht $b$ für einen beliebigen Buchstaben, $z$ für eine beliebige Ziffer und $s$ für ein beliebiges Sonderzeichen.

Rob Mieremet, CC BY-SA 3.0 NL via Wikimedia Commons

1. Angenommen, der kubanische Geheimdienst analysierte den (unverschlüsselten) Funkverkehr des bri­tischen Geheim­dienstes MI6. Ein Automat soll erkennen, sobald sich im Eingabewort die Ziffernfolge $007$ befindet.

   • 👤 Erstelle einen solchen DEA über dem Alphabet $A = \{0, 1, ... , 9\}$.
   • 👤 Verändere den DEA so, dass sowohl Wörter, die die Kennung $007$ als auch die Kennung $008$ enthalt­en, akzeptiert werden.

2. Damit James Bond nicht immer so ernst schaut, soll ein Lachautomat konstruiert werden.

   • 👤 Erstelle einen DEA über dem Alphabet $A = \{h, i , !\}$, der die folgenden Wörter akzeptiert: $hi!$, $hihi!$, $hihihi!$ usw. Formal ist das die Sprache $L_{Lachsprache} = \{ (hi)^n ! \ | \ n \in \N \}$

3. B wie in in Great Britain:

   • 👤 Erstelle einen DEA über dem Alphabet $A = \{ b \}$, der nur dann eine Fol­ge des Buchstabens $b$ akzeptiert, wenn diese aus einer Anzahl von Buchstaben besteht, die durch 3 teilbar ist.
   • 👤 Erstelle einen solchen Automaten mit möglichst wenigen Zuständen. Tipp: Es sind nur drei Zustände möglich.

🏃‍♀️ Extras:

• Variante 1: Erstelle einen DEA über dem Alphabet $A = \{0, 1, … , 9\}$, der genau solche Zahlen ak­zeptiert, die durch 3 teilbar sind. (Optional kannst du auch die Teilbarkeit durch 6 überprüfen.)
• Variante 2: Erstelle eine eigene Übungsaufgabe zu DEA und gib die Lösung an.

Das leere Worte bezeichnet ein Wort, das aus keinem Zeichen besteht. Es hat die Länge null.

Die Menge der Wörter, die vom Automaten akzeptiert werden, also die Wörter bei denen der Automat in einen akzeptierenden Endzustand gelangt, nennt man die vom Automaten akzeptierte Sprache.